Let \(\mathcal{S}\) be the surface of the cylinder (not including the top and bottom) of radius 2 for \(1 \leq z \leq 6\), oriented with outward-pointing normal (Figure 16).

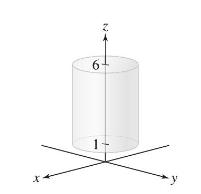
(a) Indicate with an arrow the orientation of \(\partial \mathcal{S}\) (the top and bottom circles).
(b) Verify Stokes' Theorem for \(\mathcal{S}\) and \(\mathbf{F}=\left\langle y z^{2}, 0,0ightangle\).

Transcribed Image Text:

Xx 6 1