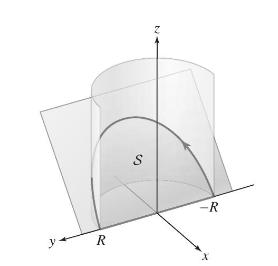
Let \(\mathcal{S}\) be the portion of the plane \(z=x\) contained in the half-cylinder of radius \(R\) depicted in Figure 17. Use Stokes' Theorem to calculate the circulation of \(\mathbf{F}=\langle z, x, y+2 zangle\) around the boundary of \(\mathcal{S}\) (a halfellipse) in the counterclockwise direction when viewed from above. Show that \(\operatorname{curl}(\mathbf{F})\) is orthogonal to the normal vector to the plane.

Transcribed Image Text:

THEOREM 1 Stokes' Theorem Let S be a surface as described earlier, and let F be a vector field whose components have continuous partial derivatives on an open region containing S. as F.dr = 1 Is The integral on the left is defined relative to the boundary orientation of 25. If S is a closed surface, then curl(F). ds curl(F) dS=0 . 1