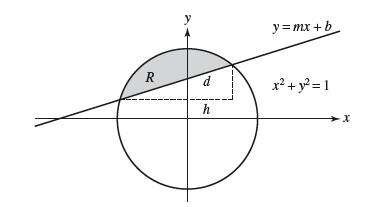
Let R be the region in the unit circle lying above the cut with the line y = mx + b (Figure 20). Assume that the points where the line intersects the circle lie above the x-axis. Use the method of Exercise 65 to show that the solid obtained by rotating R about the x-axis has volume V = π/6 hd², with h and d as in the figure.

Data From Exercise 65

Transcribed Image Text:

R y d h y=mx+b x² + y² = 1 ➤X