Pappus's Theorem (also called Guldin's Rule), which we introduced in Section 8.4 , states that the area

Question:

Pappus's Theorem (also called Guldin's Rule), which we introduced in Section 8.4 , states that the area of a surface of revolution $\mathcal{S}$ is equal to the length $L$ of the generating curve times the distance traversed by the center of mass. Use Eq. (14) to prove Pappus's Theorem. If $C$ is the graph $z=g(y)$ for $c \leq y \leq d$, then the center of mass is defined as the point $(\bar{y}, \bar{z})$ with

\[
\bar{y}=\frac{1}{L} \int_{C} y d s, \quad \bar{z}=\frac{1}{L} \int_{C} z d s
\]

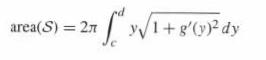
area(S) = 27 y/1+g'(y) dy