Compute the surface area of the torus in Exercise 45 using Pappus's Theorem.

Data From Exercise 45

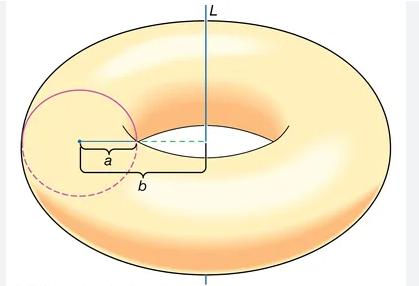
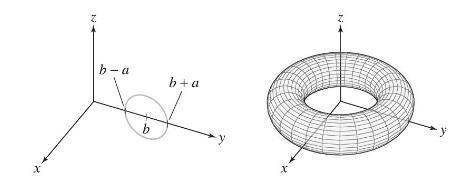
Area of a Torus Let \(\mathcal{T}\) be the torus obtained by rotating the circle in the \(y z\)-plane of radius \(a\) centered at \((0, b, 0)\) about the \(z\)-axis (Figure 23). We assume that \(b>a>0\).

(a) Use Eq. (14) to show that
\[
\operatorname{area}(\mathcal{T})=4 \pi \int_{b-a}^{b+a} \frac{a y}{\sqrt{a^{2}-(b-y)^{2}}} d y
\]

(b) Show that \(\operatorname{area}(\mathcal{T})=4 \pi^{2} a b\).

Transcribed Image Text:

a b |L