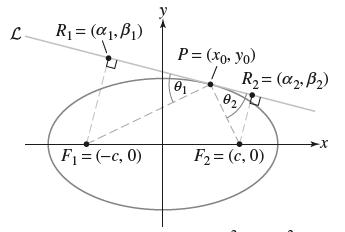
Points R 1 and R 2 in Figure 25 are defined so that F 1 R 1
Question:
Points R1 and R2 in Figure 25 are defined so that F1R1 and F2R2 are perpendicular to the tangent line.
(a) Show, with A and B as in Exercise 70, that
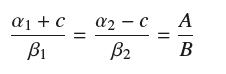
(b) Use (a) and the distance formula to show that
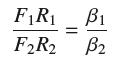
(c) Use (a) and the equation of the tangent line in Exercise 70 to show that
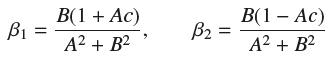
Data From Exercise 70
We prove that the focal radii at a point on an ellipse make equal angles with the tangent line L. Let P = (x0, y0) be a point on the ellipse in Figure 25 with foci F1 = (−c, 0) and F2 = (c, 0), and eccentricity e = c/a.
Show that the equation of the tangent line at P is Ax + By = 1, where A = x0/a2 and B = y0/b2.
We prove that the focal radii at a point on an ellipse make equal angles with the tangent line L. Let P = (x0, y0) be a point on the ellipse in Figure 25 with foci F1 = (−c, 0) and F2 = (c, 0), and eccentricity e = c/a.
Show that the equation of the tangent line at P is Ax + By = 1, where A = x0/a2 and B = y0/b2.
Step by Step Answer:
a From Exercise 70 the tangent line at P has equation A...View the full answer
