Prove that the length of a curve as computed using the arc length integral does not depend
Question:
Prove that the length of a curve as computed using the arc length integral does not depend on its parametrization. More precisely, let C be the curve traced by r(t) for a ≤ t ≤ b. Let ƒ (s) be a differentiable function such that ƒ(s) > 0 and ƒ(c) = a and ƒ(d) = b. Then r1(s) = r(ƒ(s)) parametrizes C for c ≤ s ≤ d. Verify that
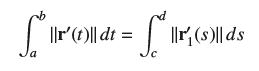
Transcribed Image Text:
S ||r' (t)|| dt = ||r(s)|| ds
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 66% (3 reviews)
Hence By the Chain Rule we have rt tr pt S rt tr yt ...View the full answer

Answered By

Shubhradeep Maity
I am an experienced and talented freelance writer passionate about creating high-quality content. I have over five years of experience working in the field and have collaborated with several renowned companies and clients in the SaaS industry.
At Herman LLC, an online collective of writers, I generated 1,000+ views on my content and created journal content for 100+ clients on finance topics. My efforts led to a 60% increase in customer engagement for finance clients through revamping website pages and email interaction.
Previously, at Gerhold, a data management platform using blockchain, I wrote and published over 50 articles on topics such as Business Finance, Scalability, and Financial Security. I managed four writing projects concurrently and increased the average salary per page from $4 to $7 in three months.
In my previous role at Bernier, I created content for 40+ clients within the finance industry, increasing sales by up to 40%.
I am an accomplished writer with a track record of delivering high-quality content on time and within budget. I am dedicated to helping my clients achieve their goals and providing exceptional results.
5.00+
1+ Reviews
10+ Question Solved
Related Book For 

Question Posted:
Students also viewed these Mathematics questions
-
Let (A, R) be a poset in which the length of a longest (maximal) chain is n 2. Let M be the set of all maximal elements in (A, R), and let B = A - M. If R' = (B B) R, prove that the length of a...
-
On Dec. 1, 2014 Pete Fiore opened Flore Consulting Services, Inc. He provides marketing seminars guaranteed to increase sales by SK. The first fiscal (calendar) year will end December 31, 2014. One...
-
The Aggie Watch Corporation manufactures watches on a conveyor belt with 6 stations. One worker stands at each station and performs the following tasks: a . Where in the process is the bottleneck? b...
-
Ten thousand dollars is deposited in a savings account at 4.6% interest compounded continuously. When will the balance triple? O within a year of investment. O In 10 years approximately. none of the...
-
What are the computational guidelines for determining whether a convertible security is to be reported as part of diluted earnings per share?
-
What is dissaving? Describe a situation that would create dissaving in an economy.
-
How Do Theories and Models Explain Management and Leadership? (pp. 4549)
-
Barbara is a sales representative for Global Fashions Inc. One of her best customers, George, places a large order for linen jackets for the coming spring season. Barbara knows that Global has had...
-
Present and future values of $1 at 3% are presented below: Suppose you would like to have $70,0007-years from now. How much must you invest today in an account that earns 6% compounded semiannually
-
The curve known as the Bernoulli spiral (Figure 7) has parametrization r(t) = (e t cos 4 t , e t sin 4t). (a) Evaluate s(1) = ||' (u) du. It is convenient to take lower limit -co because _lim_r(1) =...
-
The unit circle with the point (1, 0) removed has parametrization (see Exercise 79 in Section 11.1) Use this parametrization to compute the length of the unit circle as an improper integral. Hint:...
-
Show how the polytropic exponent n can be evaluated if you know the end state properties, (P1, V1) and (P2, V2).
-
You have been employed as a systems analyst in the information systems organization of a medium-sized consumer goods manufacturer for three years. You are quite surprised when your manager offers you...
-
For your initial post, address the following: First, introduce yourself to the class by sharing a bit about yourself, such as your preferred name or pronouns, where you are from, what your major is,...
-
Question 8 : Consider the technology of Solar Panels. Which stage of the technology life cycle S curve is this technology in. Justify why ? Question 9 : The standard Product Life Cycle has 5 stages...
-
At Benihana restaurant a man wrenched his neck while ducking a piece of flying shrimp, requiring treatment by several doctors. By that summer, doctors determined surgery was necessary to treat...
-
You have just come into an inheritance of $25,000 from a distant relative, and you want to invest it for the long term. Provide an investment portfolio that includes five different stocks. Report the...
-
Find the sum of the first 20 terms of the series 17 + 13 + 9 + g .
-
Refer to the data in QS 10-1. Based on financial considerations alone, should Helix accept this order at the special price? Explain.
-
If the solution to a system of two linear equations containing two unknowns is x = 3, y= -2, then the lines intersect at the point________.
-
If the lines that make up a system of two linear equations are coincident, then the system is________and the equations are________.
-
Verify that the values of the variables listed are solutions of the system of equations. S2x - y = 5 [5x + 2y = 8 x = 2, y = -1; (2, 1)
-
American Food Services, Incorporated leased a packaging machine from Barton and Barton Corporation. Barton and Barton completed construction of the machine on January 1 , 2 0 2 4 . The lease...
-
Which of the following statements is true? Financial measures tend to be lag indicators that report on the results of past actions. LA profit center is responsible for generating revenue, but it is...
-
Andretti Company has a single product called a Dak. The company normally produces and sells 8 0 , 0 0 0 Daks each year at a selling price of $ 5 6 per unit. The company s unit costs at this level of...

Study smarter with the SolutionInn App


