Prove that the portion of a sphere of radius R seen by an observer located at a distance d above the North Pole has area A = 2πdR²/(d + R). According to Exercise 52, the cap has surface area 2πRh. Show that h = dR/(d + R) by applying the Pythagorean Theorem to the three right triangles in Figure 22.

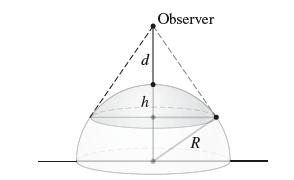
Data From Exercise 52

Show that a spherical cap of height h and radius R (Figure 19) has surface area 2πRh.

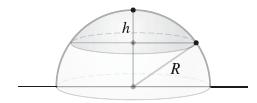
Transcribed Image Text:

h Observer R