Suppose that is a function such that (0) = 1 and for all x, '(x) =

Suppose that ƒ is a function such that ƒ(0) = 1 and for all x, ƒ'(x) = ƒ(x) and ƒ(x) > 0 (in Chapter 7, we will see that ƒ(x) is the exponential function ex). Prove that for all x ≥ 0 (each assertion follows from the previous one),

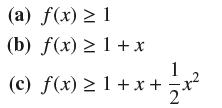
Then prove by induction that for every whole number n and all x ≥ 0,

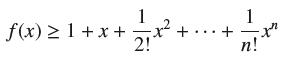
Transcribed Image Text:

(a) f(x) ≥ 1 (b) f(x) > 1 + x 1 (c) f(x) ≥ 1 + x + x²