The Second Derivative Test for critical points fails if (c) = 0. This exercise develops a Higher Derivative Test based on the sign of the

The Second Derivative Test for critical points fails if ƒ"(c) = 0. This exercise develops a Higher Derivative Test based on the sign of the first nonzero derivative. Suppose that

(a) Show, by applying L’Hôpital’s Rule n times, that

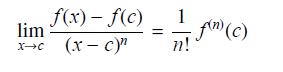
where n! = n(n − 1)(n − 2) · · · (2)(1).

(b) Use (a) to show that if n is even, then ƒ(c) is a local minimum if ƒ(n)(c) > 0 and is a local maximum if ƒ(n)(c)

(c) Use (a) to show that if n is odd, then ƒ(c) is neither a local minimum nor a local maximum.

f'(c) = f'(c)= = f(n-) (c) = 0, but f(c) # 0