The upper half of the sphere \(x^{2}+y^{2}+z^{2}=9\) has parametrization \(\Phi(r, \theta)=\left(r \cos \theta, r \sin \theta, \sqrt{9-r^{2}}ight)\) in cylindrical coordinates (Figure 3).

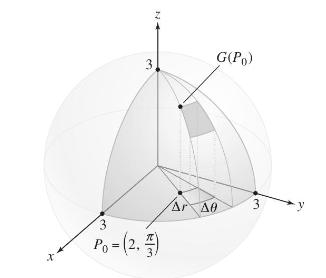
(a) Calculate the normal vector \(\mathbf{N}=\mathbf{T}_{r} \times \mathbf{T}_{\theta}\) at the point \(\Phi\left(2, \frac{\pi}{3}ight)\).
(b) Use Eq. (3) in Section 16.4 to estimate the surface area of \(\Phi(\mathcal{R})\), where \(\mathcal{R}\) is the small domain defined by
\[
2 \leq r \leq 2.1, \quad \frac{\pi}{3} \leq \theta \leq \frac{\pi}{3}+0.05
\]

Transcribed Image Text:

X 3, 3 Po=(2, 3) G(P0) 3