This exercise combined with Exercise 46 shows that for all whole numbers k, there exists a polynomial
Question:
This exercise combined with Exercise 46 shows that for all whole numbers k, there exists a polynomial P satisfying Eq. (1). The solution requires the Binomial Theorem and proof by induction.
(a) Show that δ(xk+1) = (k + 1) xk + · · · , where the dots indicate terms involving smaller powers of x.
(b) Show by induction that there exists a polynomial of degree k + 1 with leading coefficient 1/(k + 1):
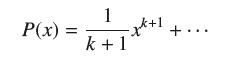
such that δP = (x + 1)k and P(0) = 0.
Data From Exercise 46
We define the first difference δ ƒ of a function ƒ by δ ƒ(x) = ƒ(x + 1) − ƒ(x).
Suppose we can find a function P such that δP(x) = (x + 1)k and P(0) = 0. Prove that P(1) = 1k , P(2) = 1k + 2k, and, more generally, for every whole number n,
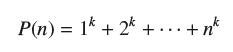
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





