To estimate the length of a circular arc of the unit circle, the seventeenth century Dutch scientist Christian Huygens used the approximation (8b a) 3, where a is the length of the chord AC of angle and b is the length of the chord A B of angle 2 (Figure 12) (a) Prove that a 2 sin( 2) and b 2 sin( ...

a By the Law of Cosines and the identity sin02 1 cos 02 0 a 1 12 cos 0 21 cos 0 4 sin 2 and s ...

To estimate the length of a circular arc of the unit circle, the seventeenth-century Dutch scientist

Question:

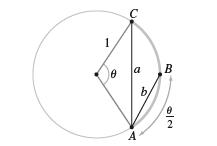
To estimate the length θ of a circular arc of the unit circle, the seventeenth-century Dutch scientist Christian Huygens used the approximation θ ≈ (8b − a)/3, where a is the length of the chord A̅C̅ of angle θ and b is the length of the chord A̅ B̅ of angle θ/2 (Figure 12).

(a) Prove that a = 2 sin(θ/2) and b = 2 sin(θ/4), and show that the Huygens approximation amounts to the approximation

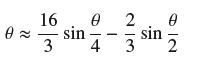
; 22 16 0 sin 3 4 2/3 sin 0 2

(b) Compute the fifth Maclaurin polynomial of the function on the right.
(c) Use the Error Bound to show that the error in the Huygens approximation is less than 0.00022|θ|⁵.

1 a A b B 7/2