We estimate integrals using Taylor polynomials. Exercise 72 is used to estimate the error. (a) Compute the
Question:
We estimate integrals using Taylor polynomials. Exercise 72 is used to estimate the error.
(a) Compute the sixth Maclaurin polynomial T6 for ƒ(x) = sin(x2) by substituting x2 in P(x) = x − x3/6, the third Maclaurin polynomial for ƒ(x) = sin x.
(b) Show that | sin(x2) − T6(x)| ≤|x|10/5!. Substitute x2 for x in the Error Bound for |sin x − P(x)|, noting that P is also the fourth Maclaurin polynomial for ƒ(x) = sin x.
(c) Use T6 to approximate ∫01/2 sin(x2) dx and find a bound for the error.
Data From Exercise 72
We estimate integrals using Taylor polynomials.
Let L > 0. Show that if two functions ƒ and g satisfy |ƒ(x) − g(x)|
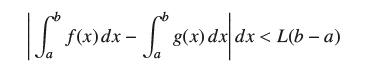
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





