Tom and Ali drive along a highway represented by the graph of in Figure 40. During

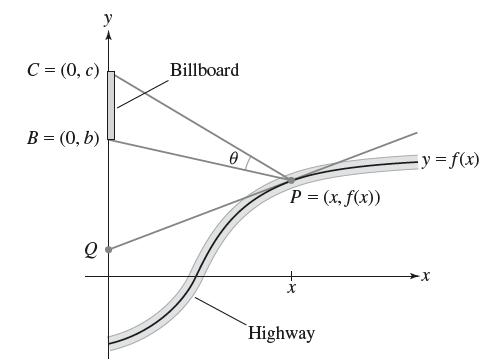
Tom and Ali drive along a highway represented by the graph of ƒ in Figure 40. During the trip, Ali views a billboard represented by the segment BC along the y-axis. Let Q be the y-intercept of the tangent line to y = ƒ(x). Show that θ is maximized at the value of x for which the angles ∠QPB and ∠QCP are equal. This generalizes Exercise 63 (c) [which corresponds to the case ƒ(x) = 0].

Data From Exercise 63 (c)

Transcribed Image Text:

C = (0, c) B = (0, b) Q Billboard 0 P = (x, f(x)) Highway - y = f(x) -X