Use Exercise 50 to prove that

Verify that Jac(I) = 1, where I is the identity map I(u, v) = (u, v).

Data From Exercise 50

Let Φ₁ : D₁ → D₂ and Φ₂ : D₂ → D₃ be C₁ maps, and let Φ₂ ◦ Φ₁ : D₁ → D₃ be the composite map. Use the Multivariable Chain Rule and Exercise 49 to show that

Data From Exercise 49

The product of 2 × 2 matrices A and B is the matrix AB defined by

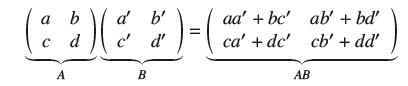
The (i, j)-entry of A is the dot product of the ith row of A and the jth column of B. Prove that det(AB) = det(A) det(B).

Jac() = Jac()-