Use Exercise 71 to prove (x) = sin x is the unique solution of Eq. (1) such

Use Exercise 71 to prove ƒ(x) = sin x is the unique solution of Eq. (1) such that ƒ(0) = 0 and ƒ'(0) = 1; and g(x) = cos x is the unique solution such that g(0) = 1 and g'(0) = 0. This result can be used to develop all the properties of the trigonometric functions “analytically”—that is, without reference to triangles.

Eq.(1)

Data From Exercise 71

Suppose that functions ƒ and g satisfy Eq. (1) and have the same initial values—that is, ƒ(0) = g(0) and ƒ'(0) = g(0). Prove that ƒ(x) = g(x) for all x. Apply Exercise 70(a) to ƒ − g.

Eq.(1)

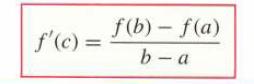
Transcribed Image Text:

f'(c) = f(b)-f(a) b-a