Use the differential equation for a leaking container, Eq. (3).

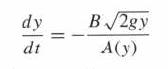
A tank has the shape of the parabola y = ax2 (where a is a constant) revolved around the y-axis. Water drains from a hole of area B m2 at the bottom of the tank.

(a) Show that the water level at time t is

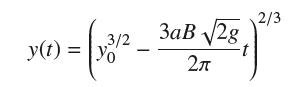
where y₀ is the water level at time t = 0.

(b) Show that if the total volume of water in the tank has volume V at time t = 0, then y₀ = √2aV/π. 

(c) Show that the tank is empty at time

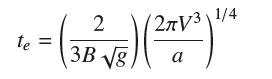
We see that for fixed initial water volume V, the time te is proportional to a^−1/4. A large value of a corresponds to a tall, thin tank. Such a tank drains more quickly than a short, wide tank of the same initial volume.

dy dt B 2gy A(y)