Verify that (mathbf{B}=operatorname{curl}(mathbf{A})) for (r>R) in the setting of Example 4. EXAMPLE 4 Vector Potential for a

Verify that \(\mathbf{B}=\operatorname{curl}(\mathbf{A})\) for \(r>R\) in the setting of Example 4.

Transcribed Image Text:

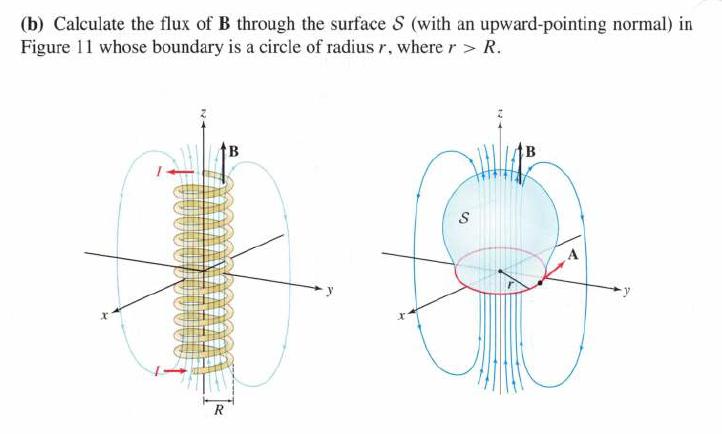
EXAMPLE 4 Vector Potential for a Solenoid An electric current I flowing through a solenoid (a tightly wound spiral of wire; see Figure 11) creates a magnetic field B. If we assume that the solenoid is infinitely long, with radius R and the z-axis as the central axis, then 0 -P A(r) = B(r) = if r > R Bk if r < R where r = (x + y2)1/2 is the distance to the z-axis, and B is a constant that depends on the current strength I and the spacing of the turns of wire. (a) Show that a vector potential for B is y RB (0) ifr> R B (-y,x,0) if r < R