We define the first difference of a function by (x) = (x +
Question:
We define the first difference δ ƒ of a function ƒ by δ ƒ(x) = ƒ(x + 1) − ƒ(x).
Show that if
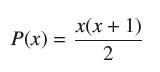
then δP = (x + 1). Then apply Exercise 46 to conclude that
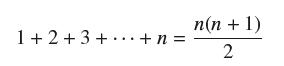
Data From Exercise 46
We define the first difference δ ƒ of a function ƒ by δ ƒ(x) = ƒ(x + 1) − ƒ(x).
Suppose we can find a function P such that δP(x) = (x + 1)k and P(0) = 0. Prove that P(1) = 1k , P(2) = 1k + 2k, and, more generally, for every whole number n,
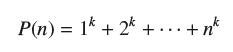
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





