Let (a) Show that P/y = Q/x. (b) Show that c F dr is not
Question:
Let
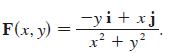
(a) Show that ∂P/∂y = ∂Q/∂x.
(b) Show that ∫c F · dr is not independent of path. [Compute ∫c1 F · dr and ∫c2 F · dr where C1 and C2 are the upper and lower halves of the circle x2 + y2 = 1 from (1, 0) to (–1, 0).] Does this contradict Theorem 6?
Data from Theorem 6
Let F = Pi + Q j be a vector field on an open simply-connected region D. Suppose that P and Q have continuous first-order derivatives and
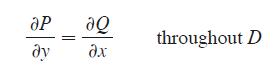
Then F is conservative.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





