Question: Use Stokes Theorem to evaluate S curl F ds.k F(x, y, z) = 2y cos zi + e x sin zj + xe

Use Stokes Theorem to evaluate ∫∫S curl F · ds.k

F(x, y, z) = 2y cos zi + exsin zj + xey k, S is the hemisphere x2 + y2 + z2 = 9, z ≥ 0, oriented upward


Data from Stokes Theorem

Let S be an oriented piecewise-smooth surface that is bounded by a simple, closed, piecewise-smooth boundary curve C with positive orientation. Let F be a vector field whose components have continuous partial derivatives on an open region in R3 that contains S. Then

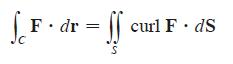
S F dr = ff S curl F. ds

S F dr = ff S curl F. dS

Step by Step Solution

★★★★★

3.42 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Fxy 2ycosisinze k In our case the boundary curve C wi... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 6th edition Questions!

Q:

The Calcio Coal Company produces coal at four mines and ships it to four power plants (P1-P4). The cost per ton of producing coal and the production capacity (in tons) for each mine are known. The...

Q:

Use Stokes Theorem to evaluate S curl F ds. F(x, y, z)= e xy cos zi + x 2 zj + xyk, S is the hemisphere x = 1 y 2 z 2 , oriented in the direction of the positive x-axis Data from Stokes Theorem...

Q:

Use Stokes Theorem to evaluate S curl F ds. F(x, y, z) = x 2 y 3 zi + sin(xyz)j + xyz k, S is the part of the cone y 2 = x 2 + z 2 that lies between the planes y = 0 and y = 3, oriented in the...

Q:

Use Stokes Theorem to evaluate C F dr. In each case C is oriented counterclockwise as viewed from above. F(x, y, z) = xyi + 2zj + 3yk, C is the curve of intersection of the plane x + z = 5 and the...

Q:

Use Stokes Theorem to evaluate S curl F dS. F(x, y, z) = ze y i + x cos y j + xz sin y k, S is the hemisphere x 2 + y 2 + z 2 = 16, y > 0, oriented in the direction of the positive y-axis

Q:

Use Stokes' Theorem to evaluate S curl F dS . F ( x , y , z ) = 2 y cos z i + ex sin z j + xey k , S is the hemisphere x 2 + y 2 + z 2 = 9 , z 0 , oriented upward.

Q:

solve the answers handwritten but please type all the final answers together in the different section after solving. Thanks. 1. [-/1 Points] DETAILS SCALCET9 16.8.004. Use Stokes' theorem to evaluate...

Q:

1. [-/0.66 Points] DETAILS MY NOTES PRACTICE ANOTHER Use Stokes' Theorem to evaluate 1/5 Curl F . as. F(x, y, z) = zeyi + x cos(y)j + xz sin(y)k, S is the hemisphere x2 + y2 + z2 = 4, y 2 0, oriented...

Q:

4 5p Use Stokes Theorem to evaluate s curl F ds Suppose F x y z ycos z e sin z xe and S is the upper hemisphere of radius 3 orient upward

Q:

I need explanation of Problem 9. Thank you in On 12. (a c Stokes' Theorem to evaluate JJ curl F . dS. (. y. z) = x'sinzity"j+ xyk, the part of the paraboloid z = 1 - x2 - y? that lies Have the...

Q:

in On 12. (a c Stokes' Theorem to evaluate JJ curl F . dS. (. y. z) = x'sinzity"j+ xyk, the part of the paraboloid z = 1 - x2 - y? that lies Have the xy-plane, oriented upward 7 2) = ze" i + x cosy j...

Q:

1. Let X be an inner product space. Using the parallelogram identity to prove by few lines the Appolonius' identity: |lz - x||2+||z y|| = ||x y|| + 2 2. Prove that the norm function f (x) ||x||:X R...

Q:

11. What is the frequency of 802.11a networking? 5.75 GHz 2.4 GHz 1.2 GHz 900 MHz 12. How many total channels are available for 802.11a wirelessnetworks? 54 23 12 11 3 13. How many total channels are...

Q:

[ - / 0 . 5 Points ] SCALCET 8 1 2 . 5 . 0 2 7 . Find an equation of the plane. The plane through the point ( 3 , - 2 , - 5 ) and parallel to the plane 8 x - y - z = 6 Need Help? 7 . [ - / 0 . 5...

Q:

=+5 Describe product-related segmentation.

Q:

Formulate a comparison test for improper integrals with infinite integrands?

Q:

(a) Use Example 2 of Section 8.02 to show that for any positive number n there is a number M such that (b) Use part (a) and Problem 46 to show that Converges? "1 "edx

Q:

Using Problem 50, prove that Converges for n > 0? x"-le* dx

Q:

Manufacturing Inc bonds have an 8.3% coupon rate, payable semiannually, and a par value of $1,000. They mature exactly 10 years from today. The yield to maturity is 11%, so the bonds now sell below...

Q:

The other category is: A. Cognitive Abilities and Judgement B. Comprehension C. Forecasting D. Synthesis

Q:

One of the determining factors regarding whether the equity method or consolidation should be used is the concept of control. How does control determine which method should be used? What are some of...