A circular curve of radius R on a highway is banked at an angle so that

A circular curve of radius R on a highway is banked at an angle θ so that a car can safely traverse the curve without skidding when there is no friction between the road and the tires. The loss of friction could occur, for example, if the road is covered with a film of water or ice. The rated speed v_R of the curve is the maximum speed that a car can attain without skidding. Suppose a car of mass m is traversing the curve at the rated speed v_R. Two forces are acting on the car: the vertical force, mg, due to the weight of the car, and a force F exerted by, and normal to, the road. The vertical component of F balances the weight of the car, so that |F| cos θ = mg. The horizontal component of F produces a centripetal force on the car so that, by Newton’s Second Law and part (d) of Problem 1,

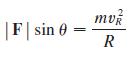
(a) Show that v²_R = Rg tan θ.

(b) Find the rated speed of a circular curve with radius 400 ft that is banked at an angle of 12°.

(c) Suppose the design engineers want to keep the banking at 12°, but wish to increase the rated speed by 50%. What should the radius of the curve be?

Transcribed Image Text:

mvk |F| sin e