(a) Find the maximum value of 

given that x₁, x₂, . . . , x_n are positive numbers and x₁ + x₂ + ∙ ∙ ∙ + xn = c, where c is a constant.

(b) Deduce from part (a) that if x₁, x₂, . . . , xn are positive numbers, then

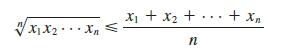
This inequality says that the geometric mean of n numbers is no larger than the arithmetic mean of the numbers. Under what circumstances are these two means equal?

Transcribed Image Text:

f(x1, x2, . .. , x,) Vx1x2 Xn %3| ..