(a) Show that, by taking logarithms, the general Cobb-Douglas function P = bL K 1 can...

(a) Show that, by taking logarithms, the general Cobb-Douglas function P = bL^αK^1−α can be expressed as

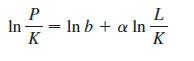
(b) If we let x − ln(L/K) and y = ln(P/K), the equation in part (a) becomes the linear equation y = αx + ln b. Use Table 2 (in Example 4) to make a table of values of ln(L/K) and ln(P/K) for the years 1899–1922. Then find the least squares regression line through the points (ln(L/Kd, ln(P/K)).

(c) Deduce that the Cobb-Douglas production function is P = 1.01L^0.75K^0.25.

Transcribed Image Text:

P In b + a In K L In K