Consider the solid region S that lies under the surface z = x 2 y and above
Question:
Consider the solid region S that lies under the surface z = x2√y and above the rectangle R = [0, 2] c [1, 4].
(a) Find a formula for the area of a cross-section of S in the plane perpendicular to the x-axis at x for 0 ≤ x ≤ 2. Then use the formula to compute the areas of the cross-sections illustrated.

(b) Find a formula for the area of a cross-section of S in the plane perpendicular to the y-axis at y for 1 ≤ y ≤ 4. Then use the formula to compute the areas of the cross-sections illustrated.
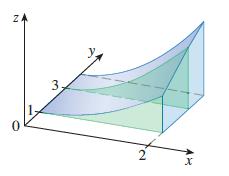
(c) Find the volume of S.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Calculus Early Transcendentals
ISBN: 9781337613927
9th Edition
Authors: James Stewart, Daniel K. Clegg, Saleem Watson, Lothar Redlin
Question Posted:





