The Wallis Product Formula for Let (a) Show that I 2n+2 I 2n+1 I
Question:
The Wallis Product Formula for π Let
![]()
(a) Show that I2n+2 ≤ I2n+1 ≤ I2n.
(b) Use Exercise 56 to show that
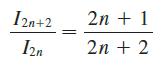
(c) Use parts (a) and (b) to show that
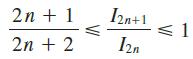
and deduce that
![]()
(d) Use part (c) and Exercises 55 and 56 to show that
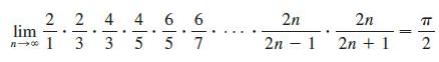
This formula is usually written as an infinite product:
![]()
and is called the Wallis product.
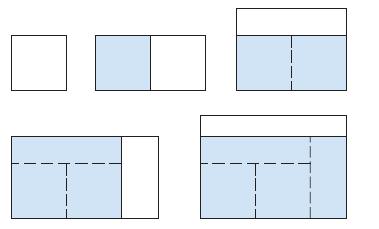
(e) We construct rectangles as follows. Start with a square of area 1 and attach rectangles of area 1 alternately beside or on top of the previous rectangle (see the figure). Find the limit of the ratios of width to height of these rectangles.
Data From Exercise 55:
(a) Use the reduction formula to show that
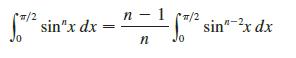
where n ≥ 2 is an integer.
(b) Use part (a) to evaluate ∫π/20 sin3x dx and ∫π/20 sin5x dx.
(c) Use part (a) to show that, for odd powers of sine,
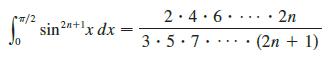
Data From Exercise 56:
Prove that, for even powers of sine,
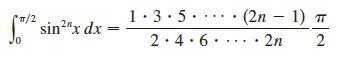
Step by Step Answer:

Calculus Early Transcendentals
ISBN: 9781337613927
9th Edition
Authors: James Stewart, Daniel K. Clegg, Saleem Watson, Lothar Redlin





