Use the following steps to show that the sequence has a limit. (The value of the limit
Question:
Use the following steps to show that the sequence
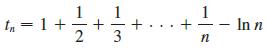
has a limit. (The value of the limit is denoted by γ and is called Euler’s constant.)
(a) Draw a picture like Figure 6 with f(x) = 1/x and interpret tn as an area [or use (5)] to show that tn > 0 for all n.
(b) Interpret
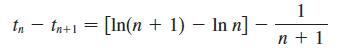
as a difference of areas to show that tn – tn+1 > 0. Therefore {tn} is a decreasing sequence.
(c) Use the Monotonic Sequence Theorem to show that {tn} is convergent.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Calculus Early Transcendentals
ISBN: 9781337613927
9th Edition
Authors: James Stewart, Daniel K. Clegg, Saleem Watson, Lothar Redlin
Question Posted:





