A spring hangs from the ceiling at equilibrium with a mass attached to its end. Suppose you pull downward on the mass and release it 10 inches below its equilibrium position with an upward push. The distance x (in inches) of the mass from its equilibrium position after t seconds is given by the function x(t) = 10 sin t - 10 cos t, where x is positive when the mass is above the equilibrium position.

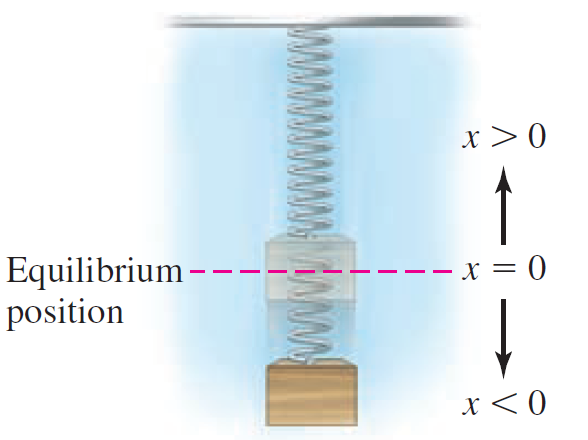
a. Graph and interpret this function.

b. Find dx/dt and interpret the meaning of this derivative.

c. At what times is the velocity of the mass zero?

d. The function given here is a model for the motion of an object on a spring. In what ways is this model unrealistic?

Equilibrium - - position -- x = 0