An integrand with trigonometric functions in the numerator and denominator can often be converted to a rational
Question:
An integrand with trigonometric functions in the numerator and denominator can often be converted to a rational integrand using the substitution u = tan (x/2) or equivalently x = 2 tan-1 u. The following relations are used in making this change of variables.
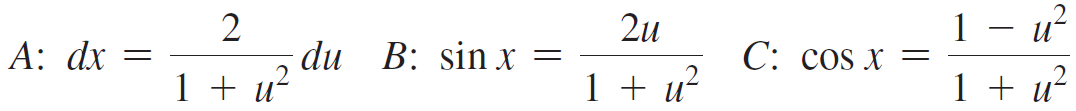
Verify relation A by differentiating x = 2 tan-1 u. Verify relations B and C using a right-triangle diagram and the double-angle formulas
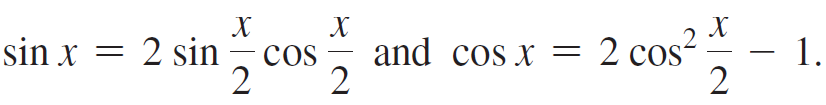
Transcribed Image Text:
и 2 du B: sin xх %— 2u |A: dx = C: cos x = 1+ и? 1+ и? 1 + и? sin x - 2 sin and cos x = 2 cos s 2 .2 cos 1. 2
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 45% (11 reviews)
If x2 tan u then dx 1 du If u ta...View the full answer

Answered By

Nicholas Maina
Throughout my tutoring journey, I've amassed a wealth of hands-on experience and honed a diverse set of skills that enable me to guide students towards mastering complex subjects. My proficiency as a tutor rests on several key pillars:
1. Subject Mastery:
With a comprehensive understanding of a wide range of subjects spanning mathematics, science, humanities, and more, I can adeptly explain intricate concepts and break them down into digestible chunks. My proficiency extends to offering real-world applications, ensuring students grasp the practical relevance of their studies.
2. Individualized Guidance:
Recognizing that every student learns differently, I tailor my approach to accommodate various learning styles and paces. Through personalized interactions, I identify a student's strengths and areas for improvement, allowing me to craft targeted lessons that foster a deeper understanding of the material.
3. Problem-Solving Facilitation:
I excel in guiding students through problem-solving processes and encouraging critical thinking and analytical skills. By walking learners through step-by-step solutions and addressing their questions in a coherent manner, I empower them to approach challenges with confidence.
4. Effective Communication:
My tutoring proficiency is founded on clear and concise communication. I have the ability to convey complex ideas in an accessible manner, fostering a strong student-tutor rapport that encourages open dialogue and fruitful discussions.
5. Adaptability and Patience:
Tutoring is a dynamic process, and I have cultivated adaptability and patience to cater to evolving learning needs. I remain patient through difficulties, adjusting my teaching methods as necessary to ensure that students overcome obstacles and achieve their goals.
6. Interactive Learning:
Interactive learning lies at the heart of my approach. By engaging students in discussions, brainstorming sessions, and interactive exercises, I foster a stimulating learning environment that encourages active participation and long-term retention.
7. Continuous Improvement:
My dedication to being an effective tutor is a journey of continuous improvement. I regularly seek feedback and stay updated on educational methodologies, integrating new insights to refine my tutoring techniques and provide an even more enriching learning experience.
In essence, my hands-on experience as a tutor equips me with the tools to facilitate comprehensive understanding, critical thinking, and academic success. I am committed to helping students realize their full potential and fostering a passion for lifelong learning.
4.90+
5+ Reviews
16+ Question Solved
Related Book For 

Calculus Early Transcendentals
ISBN: 978-0321947345
2nd edition
Authors: William L. Briggs, Lyle Cochran, Bernard Gillett
Question Posted:
Students also viewed these Mathematics questions
-
Perform the operation by first converting the numerator and denominator to scientific notation. Write the answer in scientific notation. 7,200,00/0.000009
-
Values of F cv depend on the numerator and denominator ____.
-
How can a departmental overhead system be converted to a plantwide overhead system?
-
Measuring the height of a California redwood tree is very difficult because these trees grow to heights over 300 feet. People familiar with these trees understand that the height of a California...
-
Nye Tools, incorporated in 2005, makes tools and devices for the automotive industry. The original shareholders were Andre (700 shares) and his brother Roscoe (300 shares). In 2009, Andre transferred...
-
Where is the Structure statement typically entered? a. The forms Declarations section b. The Definition section in the Code Editor window c. The forms Load event procedure d. The User-defined section...
-
Consider dot plots a and b shown above. In which plot is the difference between the sample means small relative to the variability within the sample observations? Justify your answer.
-
Alec, Daniel, William, and Stephen decide today to save for retirement. Each person wants to retire by age 65 and puts $11,000 into an account earning 10% compounded annually. Required: Calculate how...
-
C o m p r e h e n s i v e P r o b l e m C h a p t e r s 6 8 Fray Enterprises is a small business that purchases electronic personal information managers (PIM) from manufacturers and sells them to...
-
Dorothy is considering a new part-time business venture where she would monogram linens and other items. To do this, she would need to upgrade her current sewing machine. Here is what she quickly...
-
Evaluate in two ways: using partial fractions and a trigonometric substitution. Reconcile your two answers. dx for x > 1, x 1
-
An integrand with trigonometric functions in the numerator and denominator can often be converted to a rational integrand using the substitution u = tan (x/2) or equivalently x = 2 tan -1 u. The...
-
Calculate the mass of silver deposited at the cathode during electrolysis when a current of 1.80 A flows through an aqueous solution of silver nitrate for 45.0 min. (A r value: [Ag] = 108; F = 96 500...
-
The English statistician Karl Pearson (1857-1936) introduced a formula for the skewness of a distribution. P = 3 ( x median ) s Pearson's index of skewness Most distributions have an index of...
-
You are to specify an orifice meter for measuring the flow rate of a $35^{\circ} \mathrm{API}$ distillate $(\mathrm{SG}=0.85$ ) flowing in a $2 \mathrm{in}$. sch 160 pipe at $70^{\circ} \mathrm{F}$....
-
Let $\theta$ and $\phi$ be the polar coordinates. Introduce the complex numbers $z$ and $\bar{z}$, where $$\begin{equation*} z=e^{i \phi} \tan (\theta / 2) \equiv \xi+i \eta \tag{5.393}...
-
Suppose the profit \(P\) (in dollars) of a certain item is given by \(P=1.25 x-850\), where \(x\) is the number of items sold. a. Graph this profit relationship. b. Interpret the value of \(P\) when...
-
(a) Draw a simplified ray diagram showing the three principal rays for an object located outside the focal length of a diverging lens. (b) Is the image real or virtual? (c) Is it upright or inverted?...
-
Why is a value income statement useful to managers?
-
Should U.S. antidumping laws be stated in terms of average total costs or average variable costs?
-
Use the formal definition of limit to prove that the function has a continuous extension to the given value of x. f(x) x - 1 x + 1' I- X x = -1
-
Find the limit of each rational function (a) As x and (b) As x -. f(x) 2x + 7 x3 x = x + x + 7
-
Prove the limit Constant Multiple Rule: for any constant k. lim kf(x) = k lim f(x) X-C X-C
-
1-The yield to maturity will be greater than the coupon rate when a bond is selling at a premium. Select one: a. False b. True 2-Which one of the following would have the greatest present value,...
-
! Required information [ The following information applies to the questions displayed below. ] Year 1 total cash dividends Year 2 total cash dividends Year 3 total cash dividends Year 4 total cash...
-
WISE-HOLLAND CORPORATION On June 15, 2013, Marianne Wise and Dory Holland came to your office for an initial meeting. The primary purpose of the meeting was to discuss Wise-Holland Corporation's tax...

Study smarter with the SolutionInn App


