At Earth’s surface, the acceleration due to gravity is approximately g = 9.8 m/s² (with local variations). However, the acceleration decreases with distance from the surface according to Newton’s law of gravitation. At a distance of y meters from Earth’s surface, the acceleration is given by

where R = 6.4 × 10⁶ m is the radius of Earth.

a. Suppose a projectile is launched upward with an initial velocity of v₀ m/s. Let v(t) be its velocity and y(t) its height (in meters) above the surface t seconds after the launch. Neglecting forces such as air resistance, explain why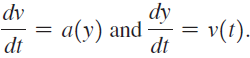

b. Use the Chain Rule to show that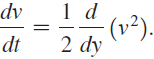

c. Show that the equation of motion for the projectile is where a(y) is given previously.

d. Integrate both sides of the equation in part (c) with respect to y using the fact that when y = 0, v = v₀. Show that

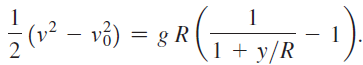
e. When the projectile reaches its maximum height, v = 0. Use this fact to determine that the maximum height is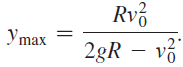 

f. Graph y_max as a function of v₀. What is the maximum height when v₀ = 500 m/s, 1500 m/s, and 5 km/s?

g. Show that the value of v₀ needed to put the projectile into orbit (called the escape velocity) is √2gR.

Transcribed Image Text:

a(y) (1 + y/R)² || dv a(y) and |dt dy v(1). dt