Question: Consider the expression where the process continues indefinitely. a. Show that this expression can be built in steps using the recurrence relation a 0 =
Consider the expression 
where the process continues indefinitely.
a. Show that this expression can be built in steps using the recurrence relation a0 = 1, an + 1 = ?1 + an, for n = 0, 1, 2, 3, ?. . . Explain why the value of the expression can be interpreted as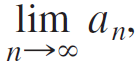 
provided the limit exists.
b. Evaluate the first five terms of the sequence {an}.?
c. Estimate the limit of the sequence. Compare your estimate with (1 + ?5)/2, a number known as the golden mean.
d. Assuming the limit exists, use the method of Example 5 to determine the limit exactly.
e. Repeat the preceding analysis for the expression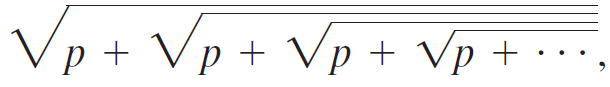
where p > 0. Make a table showing the approximate value of this expression for various values of p. Does the expression seem to have a limit for all positive values of p?
V1 + V1 + V + VI lim an n Vp + Vp + Vp + p +
Step by Step Solution
3.40 Rating (166 Votes )
There are 3 Steps involved in it
a If we cut off the expression after n square roots we get an from the re... View full answer
Get step-by-step solutions from verified subject matter experts
Study Help