Question: Let R be the region bounded by y = 1/x p and the x-axis on the interval [1, a], where p > 0 and a

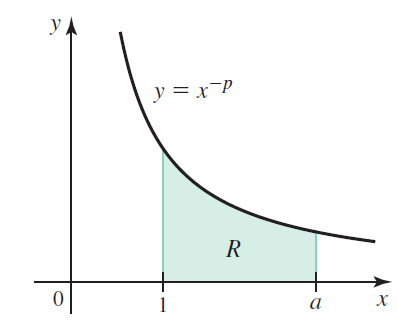
Let R be the region bounded by y = 1/x^p and the x-axis on the interval [1, a], where p > 0 and a > 1 (see figure). Let V_x and V_y be the volumes of the solids generated when R is revolved about the x- and y-axes, respectively.

a. With a = 2 and p = 1, which is greater, V_x or V_y?

b. With a = 4 and p = 3, which is greater, V_x or V_y?

c. Find a general expression for Vx in terms of a and p. Note that p = 1/2 is a special case. What is V_x when p = 1/2?

d. Find a general expression for V_y in terms of a and p. Note that p = 2 is a special case. What is V_y when p = 2?

e. Explain how parts (c) and (d) demonstrate that 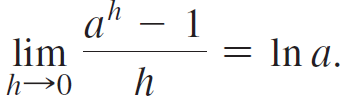a' lim - 1 In a.

f. Find any values of a and p for which V_x > V_y.

УА y, у—х Р х

a' lim - 1 In a. y,

Step by Step Solution

★★★★★

3.45 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

12 dx n1x 7 2 a V b V Vy 2 2 S c4 16 dx 255 1024 T Vy 2 c V xxdx 2 so Vy V I 4 ra 1220 I I ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus Early Transcendentals Questions!

This Quiz: 3 pts possible Attleboro Chemical Company currently operates three manufacturing plants in Colorado, Utah, and Arizona. Annual carbon emissions for these plants in the first quarter of...

Let R be the region bounded by the following curves. Use the disk method to find the volume of the solid generated when R is revolved about the x-axis. y = 0, x = 0, and x = 1/2 y = 0, x = 0, and x y...

Let R be the region bounded by the curve y = x + a (with a > 0), the y-axis, and the x-axis. Let S be the solid generated by rotating R about the y-axis. Let T be the inscribed cone that has the same...

Let R be the region bounded by the following curves. Let S be the solid generated when R is revolved about the given axis. If possible, find the volume of S by both the disk/washer and shell methods....

Reference: given by school Course: AP Calculus BC Calculator Lab S-3 You may use a calculator for any of the following problems, but be sure to show the set-up for your calculations and work. You may...

Need help solving this questions. Please show all steps. Find the area of the surface generated when the given curve is revolved about the given axis. 7% + e -7x\\ 14 e , for - 4x4; about the x-axis...

Let ftx) = + -2 and let R be the region bounded by the graph off and the xaxis on the 4 8x . ' interval [1, 4]. a. Fund the area of the surface generated when the graph of f on [1, 4] is revolved...

Let P(a, a 2 ), a > 0, be any point on the part of the parabola y = x 2 in the first quadrant, and let R be the region bounded by the parabola and the normal line through P. (See the figure.) Show...

I need help with these Find the local maximum and local minimum values of fusing both the First and Second Derivative Tests. f(x) = 8 + 9x2 6x3 A box with a square base and open top must have a...

1. For 0 5 ts 8, a particle moves along the x-axis so that its velocity v at time t, for given by v(t) = eD-Ei 'l. The particle is at position X = 4 at time t: 0. Part A: Write, but do not evaluate,...

In Boca Company, total material costs are $32,000, and total conversion costs are $54,000. Equivalent units of production are materials 10,000 and conversion costs 12,000. Compute the unit costs for...

Weak form efficiency says past information is already reflected in the stock price past and present information is already reflected in the stock price all public and private information is already...

sion 1 1 Not yet answered Marked out of 4 . 0 3 Flag question ich of the following statements is true regarding current manufacturing companies? ect ones A . Most production labor time is spent...

9. What is the duration of a portfolio consisting of one of each of the bonds listed in problem 7?

Use Theorem 15 to find the torsion of the given curve at a general point and at the point corresponding to t = 0. r(t) = (e t , e t , t)

Use Formula 14 to find the torsion at the given value of t. r(t) = (r, 21, 1), t- 1 2t,

(a) Show that dB/ds is perpendicular to B. (b) Show that dB/ds is perpendicular to T. (c) Deduce from parts (a) and (b) that dB/ds is parallel to N.

A company has total assets of $549,000, current assets of $49,000, current liabilities of $101,000, long-term debt of $209,000, and net income of $61,000. What is the company's return on assets?...

If you place a market buy order for 100 shares, at what price will it be filled? (Round your onswer to 2 decimal places.) b. If you place a market sell order for 100 shares, at what price will it be...

If Z a/2 = 2.25400, determine the proportion of (1-a) 100% confidence intervals that will not capture u when the confidence intervals are computed as m+/- A a/2 (O m )?