Pick two positive numbers a₀ and b₀ with a₀ > b₀, and write out the first few terms of the two sequences {a_n} and {b_n}:

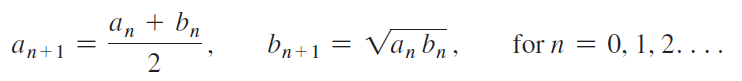
Recall that the arithmetic mean A = (p + q)/2 and the geometric mean G = ?pq of two positive numbers p and q satisfy A ? G.

a. Show that a_n > b_n for all n.

b. Show that {a_n} is a decreasing sequence and {b_n} is an increasing sequence.c. Conclude that {a_n} and {b_n} converge.d. Show that a_{n + 1} - b_{n + 1}n - b_n)/2 and conclude that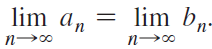The common value of these limits is called the arithmetic-geometric mean of a₀ and b₀, denoted AGM(a₀, b₀).

e. Estimate AGM(12, 20). Estimate Gauss? constant 1/AGM(1, ?2).

an+1 an + b 2 bn+1 = Van bn, for n = 0, 1, 2.... lim an n = lim b, n n