Here is a fascinating (unsolved) problem known as the hailstone problem (or the Ulam Conjecture or the Collatz Conjecture). It involves sequences in two different ways. First, choose a positive integer N and call it a₀. This is the seed of a sequence. The rest of the sequence is generated as follows: For n = 0, 1, 2, ?. . .

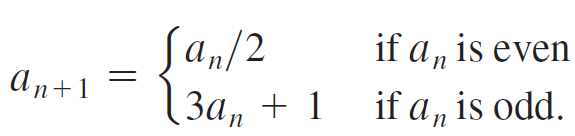
However, if a_n = 1 for any n, then the sequence terminates.?

a. Compute the sequence that results from the seeds N = 2, 3, 4, . . ., 10. You should verify that in all these cases, the sequence eventually terminates. The hailstone conjecture (still unproved) states that for all positive integers N, the sequence terminates after a finite number of terms.

b. Now define the hailstone sequence {H_k}, which is the number of terms needed for the sequence {a_n} to terminate starting with a seed of k. Verify that H₂ = 1, H₃ = 7, and H₄ = 2.

c. Plot as many terms of the hailstone sequence as is feasible. How did the sequence get its name? Does the conjecture appear to be true?

an+1 Jan/2 if an is even (3an + 1 if an is odd.