Show that in the following steps. a. Note that n! = n(n - 1)(n - 2)

Question:

Show that 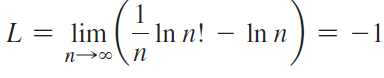|L = lim - In n! – In n in the following steps.

a. Note that n! = n(n - 1)(n - 2) · · · · 1 and use ln (ab) = ln a + ln b to show that 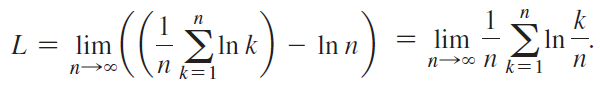(:ż--)- nk) = lim In- - Σnk k=1 L = lim In n n→0 N k=1

b. Identify the limit of this sum as a Riemann sum for 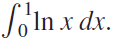Integrate this improper integral by parts and reach the desired conclusion.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Calculus Early Transcendentals

ISBN: 978-0321947345

2nd edition

Authors: William L. Briggs, Lyle Cochran, Bernard Gillett

See More Books

Question Posted: Apr 06, 2019 01:17 PM

See More Questions

Show that R 2 = span -1
Show that R 3 = span 1 1 1 1 1
Show that in the following steps. a. Integrate by parts with u = x ln x. b. Change variables by letting y = 1/x. c. Show that (and that both integrals converge). Conclude that d. Evaluate the...
For each of the following, indicate whether the item would be reported on the balance sheet (B/S), reported on the income statement (I/S), or not shown in the financial statements (Not) and whether...
Jasmine Park encountered her boss, Rick Gompers, at the pop machine in the lobby. Rick is the vice president of marketing at Down South Lures Corporation. Jasmine was puzzled by some calculations she...
Apple, Inc. manufactures and markets mobile phones, personal computers, and related software. The following data were taken from the companys 2018 and 2015 annual reports. All dollar amounts are in...
Discuss the statement that theoretical justification of measurement is the most important measurement selection criterion in FCA.
Purchasing Survey asked purchasing professionals what sales traits impressed them most in a sales representative. Seventy-eight percent selected "thoroughness." Forty percent responded "knowledge of...
A company that currently does not pay dividends on its stock is expected to begin paying a constant $3 dividend 6 years from now. The company is expected to maintain this constant dividend for 10...
Amadeus Corporation is considering the issue of a new product to be added to its product mix. They hired you, a recent business graduate from MacEwan, for conducting the analysis. The production line...
The gamma function is defined by for p not equal to zero or a negative integer. a. Use the reduction formula to show that (p factorial). b. Use the substitution x = u 2 and the fact that to show that...
Evaluate the following integrals. |ron x*(In x + 1) dx, a > 0
Describe how a businessperson could be an effective leader yet an ineffective manager. Also describe how a businessperson could be an effective manager yet an ineffective leader.
Write out the form of the partial fraction decomposition of the function (See Example ). Do not determine the numerical values of the coefficients. (If the partial fraction decomposition does not...
Below is the actual assignment information. Here is where you will submit your event for approval. It is not graded, but you will need it to be marked complete in order to submit your paper, so...
3. (20 points) A researcher is interested in whether the phonics method of teaching reading is more or less effective than the sight method, depending on what grade the child is in. Twenty children...
Let A and B be the matrices given below: -5 9 -7 A= 8 -1 -3 B=9 6 -1 8 -1 -7. 0 Perform the following matrix operations and enter the entries below: -4A = A-4B = 5A-3B=
The product business can be isolated into four principal classes: programming administrations, framework administrations, open source and SaaS. The accompanying depicts the classifications of...
Indicate the net effect (+ for increase; for decrease; 0 for no effect) of each of the following transactions on each part of the accounting equation, Assets = Liabilities + Equity. For example, for...
Why should you not model a decision variable as a random variable with a probability distribution?
Describe geometrically when a function typically does not have a derivative at a point.
A bus will hold 60 people. The number x of people per trip who use the bus is related to the fare charged (p dollars) by the law p = [3 - (x/40)] 2 . Write an expression for the total revenue r(x)...
Find the linearizations of the following functions at x = 0. a. sin x b. cos x c. tan x d. e x e. ln (1 + x)
Bought an old van for 4000 from Peters promising to pay laterwhat is the transactions
Company has a following trade credit policy 1/10 N45. If you can borrow from a bank at 9,5% annual rate, would it be beneficial to borrow money and pay off invoices earlier?
Given the following exchange rates, which of the multiple-choice choices represents a potentially profitable inter-market arbitrage opportunity? 129.87/$1.1226/$0.00864/ 114.96/ B $0.8908/ (C)...

Show that in the following steps. a. Note that n! = n(n - 1)(n - 2)

Question:

|L = lim - In n! – In n (:ż--)- nk) = lim In- - Σnk k=1 L = lim In n n→0 N k=1

Step by Step Answer:

a We have In n In n 1 ln k Inn 1 Ink ...View the full answer

Calculus Early Transcendentals

Students also viewed these Mathematics questions