Suppose water flows in a thin sheet over the xy-plane with a uniform velocity given by the vector v = (1, 2); this means that at all points of the plane, the velocity of the water has components 1 m/s in the x-direction and 2 m/s in the y-direction (see figure). Let C be an imaginary unit circle (that does not interfere with the flow).

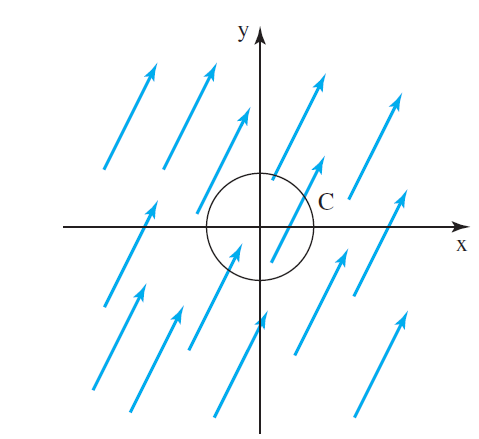
a. Show that at the point (x, y) on the circle C, the outwardpointing unit vector normal to C is n = (x, y).

b. Show that at the point (cos θ, sin θ) on the circle C, the outward pointing unit vector normal to C is also n = (cos θ, sin θ). 

c. Find all points on C at which the velocity is normal to C.

d. Find all points on C at which the velocity is tangential to C.

e. At each point on C, find the component of v normal to C. Express the answer as a function of (x, y) and as a function of θ.

f. What is the net flow through the circle? That is, does water accumulate inside the circle?

Transcribed Image Text:

y C X