Use the following definition for the nonexistence of a limit Assume f is defined for all values of x near a, except possibly at a We write if for some 0, there is no value of 0 satisfying the condition f(x) L whenever 0 x a Let Prove that does not exist for any value of a Assume for some values of ...

Suppose that exists and is equal to L Let 12 By the definition of limit there must be a numbe ...

Use the following definition for the nonexistence of a limit. Assume f is defined for all values

Question:

Use the following definition for the nonexistence of a limit. Assume f is defined for all values of x near a, except possibly at a. We write 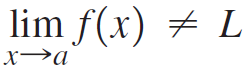|lim f(x) L if for some ε > 0, there is no value of δ > 0 satisfying the condition

|f(x) - L| < ε whenever 0 < |x - a| < δ

Let

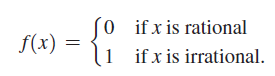
(0 ifx is rational f(x) = so if x is irrational.

Prove that 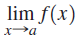does not exist for any value of a. Assume 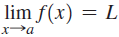for some values of a and L and let ε = 1/2.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Calculus Early Transcendentals

ISBN: 978-0321947345

2nd edition

Authors: William L. Briggs, Lyle Cochran, Bernard Gillett

See More Books

Question Posted: Feb 08, 2019 09:46 AM

See More Questions

Suppose f is defined for all values of x near a, except possibly at a. Assume for any integer N > 0 there is another integer M > 0 such that |f(x) - L| < 1/N whenever |x - a| < 1/M. Prove that using...
Prove that does not exist but that lim cos( 1/x)
ToolsCorp Corporation is a fictitious company that does not exist anywhere. Suppose, it is located in Tennessee. As members of the senior management team of ToolsCorp Corporation. Prepare a neat and...
The Illinois State University Alumni Association is having two Baseball Day events this year. The purpose of the events is to both foster relationships between ISU alums and to also raise money for...
At January 1, 2015, Bordeaux Inc. reported the following information on its statement of financial position: Accounts receivable ..................................... $480,000 Allowance for doubtful...
Give an example of a company that needs to center purpose as a matter of urgency.
In a random sample of 300 male professionals it is found that 40% play golf, 60% play soccer and 30% play both golf and soccer. Find the probability that a person selected at random from this sample...
Wallis Company manufactures only one product and uses a standard cost system. The company uses a predetermined plant wide overhead rate that relies on direct labor-hours as the allocation base. All...
17. The following data was obtained from orthogonal turning of PEEK and short- fiber-reinforced PEEK (C/PEEK, V = 0.3) [24]. Refer to Fig. 2.2 for definition of cutting variables. The cutting...
Superior Interiors is owned and operated by Ken Lopez, an interior decorator. In the ledger of Superior Interiors, the first digit of the account number indicates its major account classification...
Use the following definition for the nonexistence of a limit. Assume f is defined for all values of x near a, except possibly at a. We write if for some > 0, there is no value of > 0 satisfying the...
Suppose f is continuous at a and assume f(a) > 0. Show that there is a positive number > 0 for which f(x) > 0 for all values of x in (a - , a + ). (In other words, f is positive for all values of x...
If the distribution of Y is b(n, 0.5), give a lower bound for P(|Y/n 0.5| < 0.08) when (a) n = 100. (b) n = 500. (c) n = 1000.
A block of inertia $m$ is attached to a light string wound around a uniform disk also of inertia $m$ (Figure P11.74). The disk has radius $R$ and rotates on a fixed horizontal axle through its...
A uniform disk of mass $m$ and radius $R$ lies in a vertical plane and is pivoted about a point a distance $\ell_{\mathrm{cm}}$ from its center of mass (Figure P15.58). When given a small...
Two coherent sources of water waves of frequency $f$ and speed $c$ are a distance $d$ apart and equal in amplitude. Nodal lines exist where the path lengths from the sources differ by an odd...
Given that the speed of sound waves in dry air is $343 \mathrm{~m} / \mathrm{s}$, determine the wavelengths at the lower and upper ends of the audible frequency range \((20 \mathrm{~Hz}-20...
When your mother shouted at you to come inside when you were a kid, how could you hear her when you were around a corner?
National Computers (NC) and Hightech Ltd. (HT), two unrelated companies, agreed to share the latest technology in allowing individuals with visual impairments to use voice recognition software...
Calculate the Lagrange polynomial P 2 (x) for the values (1.00) = 1.0000, (1.02) = 0.9888, (1.04) = 0.9784 of the gamma function [(24) in App. A3.1] and from it approximations of (1.01) and (1.03).
Use the guidelines of this section to sketch the curve. y = x + cos x
Use the guidelines of this section to sketch the curve. y = x tan x, -7/2
Use the guidelines of this section to sketch the curve. 2sinx, 0
Mrs. Sam Taffer was a brilliant engineer at IBM and made a lot of money from stock options. Since then, she has worked as a musician and raised her two sons. She wishes to have most of her property...
Miller Company ended its fiscal year on June 30, 2017. The company's adjusted trial balance as of the end of its fiscal year is shown below. MILLER COMPANY Adjusted Trial Balance June 30, 2017...
What depreciation method is used to write off property, plant and equipment? Regarding the triple bottom line, what information did the company disclose about environmental matters in the reports?...

Use the following definition for the nonexistence of a limit. Assume f is defined for all values

Question:

|lim f(x) L (0 ifx is rational f(x) = so if x is irrational.

Step by Step Answer:

Suppose that exists and is equal to L Let 12 By the definition of limit there must be a numbe...View the full answer

Calculus Early Transcendentals

Students also viewed these Mathematics questions