Using the background given in Exercise 62, assume the resistance is given by f(v) = -Rv, where R > 0 is a drag coefficient (an assumption often made for a heavy medium such as water or oil).

a. Show that the equation can be written in the form v'(t) = g - bv, where b = R/m.

b. For what (positive) value of v is v'(t) = 0? (This equilibrium solution is called the terminal velocity.)

c. Find the solution of this separable equation assuming v(0) = 0 and 0 < v < g/b. 

d. Graph the solution found in part (c) with g = 9.8 m/s², m = 1 kg, and R = 0.1 kg/s, and verify that the terminal velocity agrees with the value found in part (b).

Data from Exercise 62

An object in free fall may be modeled by assuming that the only forces at work are the gravitational force and resistance (friction due to the medium in which the object falls). By Newton’s second law (mass × acceleration = the sum of the external forces), the velocity of the object satisfies the differential equation

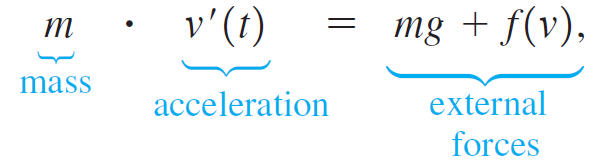
where f is a function that models the resistance and the positive direction is downward. One common assumption (often used for motion in air) is that f(v) = -kv², where k > 0 is a drag coefficient.

v'(t) mg + f(v), mass external acceleration forces ||