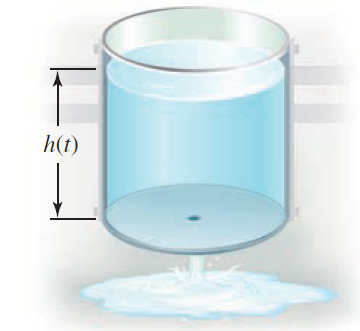
An open cylindrical tank initially filled with water drains through a hole in the bottom of the tank according to Torricelli’s Law (see figure). If h(t) is the depth of water in the tank for t ≥ 0, then Torricelli’s Law implies h'(t) = 2k√h, where k is a constant that includes the acceleration due to gravity, the radius of the tank, and the radius of the drain. Assume that the initial depth of the water is h(0) = H. 

a. Find the general solution of the equation.

b. Find the solution in the case that k = 0.1 and H = 0.5 m.

c. In general, how long does it take the tank to drain in terms of k and H?

Transcribed Image Text:

h(t)