1. Calculate the number of years to reduce pollution to 50%, 25%, and 1% of its current...
Question:
1. Calculate the number of years to reduce pollution to 50%, 25%, and 1% of its current level in Lake Erie, which has a volume of 458 cm3 and an output flow rate of 5,550,720 liter/sec.
2. Repeat Exercise 1 for Lake Michigan, which has a volume of 4871 cm3 and an output flow rate of 5,012,640 liter/sec.
3. Repeat Exercise 1 for Lake Ontario, which has a volume of 1636 cm3 and an output flow rate of 6,626,880 liter/sec.
4. We claim that the equation for C(t) given in this Extended Application is a solution of the differential equation in the Application.
(a) To show this, multiply both sides of the differential equation by ekt and then differentiate both sides with respect to t. Remember from Section 7.4 on the Fundamental Theorem of Calculus that you can differentiate an integral by using the version of the Fundamental Theorem that says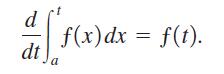
(b) When you substitute t = 0 into the right-hand side of the equation for C(t), you should get C(0). Do you? What happens to the integral? What happens to the factor of e-kt?
(c) What is the value of k for Lake Michigan? What percent of the water in Lake Michigan is replaced each year by inflow?
5. Suppose that instead of assuming that all pollution inflow immediately ceases, we model I(t) by a decaying exponential of the form ae-pt, where p is a constant that tells us how fast the inflow is being cleaned of pollution. To simplify things, we’ll also assume that initially the inflow and the lake have the same pollution concentration, so a = C(0). Now substitute C(0)e-px for I(x) in the equation for C(t), and evaluate the integral as a function of t.
6. When you simplify the right-hand side of the equation for C(t) using your new expression for the integral, and then factor out and divide by C(0), you’ll get the following expression for the ratio C(t)/C(0):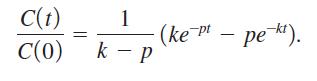
(a) Suppose that for Lake Michigan the constant p is equal to 0.02. Use a graph of the ratio C(t)/C(0) to estimate how long it will take to reduce pollution to 50% of its current value. How does this compare with the time, assuming pollution-free inflow?
(b) If the constant p has the value 0 for Lake Michigan, what does that tell you about the pollution level in the inflow? In this case, what happens to the ratio C(t)/C(0) over time?
Step by Step Answer:
1 2 3 4 a b Substituting t 0 in both sides of produces PL0 on both sides On the righ...View the full answer
