1. Find values for S and R that satisfy S = 0.3R and 0.2 (100 + S) = R. Show that these solutions give the same stipend and rent as found by summing the infinite series.

2. Suppose that instead of a stipend increase of $100, the state cuts Mr. Jones’s stipend by $50. Assuming that Mr. Jones is able to convince his landlord that he should have his rent decreased by 20% of the change, this also leads to an infinite cycle of stipend and rent changes. Express his stipend and rent as infinite series, and find the sum of each series.

3. Eastville is located 12 miles from Westville. The town councils decide to pool resources and build a single fire station to serve the needs of both towns. The negotiations on where to build the fire station start with both towns proposing the fire station be built in their town. The impasse is broken when Eastville proposes to move the site halfway to Westville, i.e., 6 miles to the west. Westville in turn proposes to move the site halfway to the Eastville proposed site, i.e., 3 miles to the east. This sets off an infinite round of negotiations in which each party proposes moving the site halfway toward the other’s previous proposal. Give an infinite series expressing the changes in location proposed by Eastville, and give a similar series for the changes proposed by Westville. Where is the fire station eventually located?

4. After building the fire station in Exercise 3, there was enough money left over for a swimming pool. This time, Eastville and Westville approach the negotiations more warily. Eastville starts by suggesting the pool be located just 1/3 of the way toward Westville. From that point on, Westville agrees to split the difference, while at every stage, Eastville proposes moving the pool just 1/3 of the way toward Westville’s last proposal. Are the towns able to reach an agreement on the final location of the pool?

5. The sum of the series for the stipend paid to Mr. Jones is approximately $1,106.3829787. Understandably, an accountant for the State of New York would view this as needless precision. To gain an appreciation of how quickly geometric series converge, particularly with a small value of R, like 0.06, use a calculator to answer the following questions. How many terms of the series do you need to add up so that the sum is within one dollar of the final answer? How many terms do you need to add up to be within a penny of the final answer?
6. Not all series converge as quickly as geometric series. We know from Section 12.5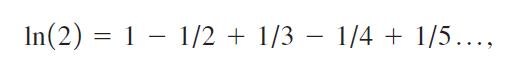

so the nth term of this series is (-1)ⁿ⁺¹/n. Use the website WolframAlpha.com to decide how many terms you need to add up so the sum is within 0.01 of ln (2). To sum a series on WolframAlpha.com, enter the following: 

sum from n = to .

Transcribed Image Text:

In(2) = 1 1 - 1/2 + 1/3 1/4 + 1/5...,