Suppose that the rate of consumption of a natural resource is c′(t), where  c′(t) = ke^rt. Here t is time in years, r is a constant, and k is the consumption in the year when t = 0. In 2020, an oil company sold 1.2 billion barrels of oil. Assume that r = 0.04.
(a) Write  c′(t) for the oil company, letting t = 0 represent 2020.
(b) Set up a definite integral for the amount of oil that the company will sell in the next 10 years.
(c) Evaluate the definite integral of part (b).
(d) The company has about 20 billion barrels of oil in reserve. To find the number of years that this amount will last, solve the equation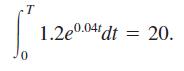

(e) Rework part (d), assuming that r = 0.02.

Transcribed Image Text:

-T So 1.2e0.04t dt = 20.