The idea of the average value of a function, discussed earlier for functions of the form y

Question:

The idea of the average value of a function, discussed earlier for functions of the form y = f (x), can be extended to functions of more than one independent variable. For a function z = f (x, y), he average value of f over a region R is defined as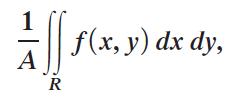

where A is the area of the region R. Find the average value for each function over the regions R having the given boundaries.

ƒ(x, y) = e^2x+y; 1 ≤ x ≤ 2, 2 ≤ y ≤ 3

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Calculus With Applications

ISBN: 9780135871348

12th Edition

Authors: Margaret L. Lial

See More Books

Question Posted: Jan 19, 2023 03:13 AM

See More Questions

The idea of the average value of a function, discussed earlier for functions of the form y = f (x), can be extended to functions of more than one independent variable. For a function z = f (x, y), he...
The idea of the average value of a function, discussed earlier for functions of the form y = f (x), can be extended to functions of more than one independent variable. For a function z = f (x, y), he...
The idea of the average value of a function, discussed earlier for functions of the form y = f (x), can be extended to functions of more than one independent variable. For a function z = f (x, y), he...
CFR is a manufacturer of Industrial machines. During 2020, CFR launched a new machine with model name Omega. Each unit of Omega is being sold for Rs. 10 million payable upon delivery. Revenue from...
Perform a value analysis on the following items: a. A stapler. b. A mouse for computer operation. c. A desk for use by students for studying.
An understatement of ending inventory in the year 20-1 will cause the owners equity account at the end of the year 20-2, assuming no other errors, to be (a) understated. (c) overstated. (b) correctly...
Name the five stages in the consumer decision process.
Use the Sweet Valley data from Problem P14-41B. In Problem P14-41b The 2018 income statement and comparative balance sheet of Sweet Valley, Inc. follow: SWEET VALLEY, INC. Income Statement Year Ended...
0 List and explain all the conditions needed to identity normal Contango and Backwarciation market? How do you satisfy those conditions
Recall from the Volume and Average Value section in the previous chapter that volume could be found with a single integral. In this section volume is found using a double integral. Explain when...
Evaluate each iterated integral. -35 [[2 (2x + 6y + y) dy dx
Solve each equation. e x = 1/e 5
You are an external auditor in a firm that undertakes the audit of Canadian Life and Mutual (CLM), a large, Montreal-based financial institution. CLM relies heavily on its computer-based information...
You need to temporarily increase the feed rate to an existing column without flooding. Since the column is now operating at about $90 \%$ of flooding, you must vary some operating parameter. The...
Consider, again, the clothing data set. Obtain the three summary plots of the sample cross-correlations for lags 1 to 21.
Based on the dangling-else discussion in Exercise 3.27, modify the following code to produce the output shown. Use proper indentation techniques. You must not make any additional changes other than...
Consider the random process $U(t)=A$, where $A$ is a random variable uniformly distributed on $(-1,1)$. (a) Sketch some sample functions of this process. (b) Find the time autocorrelation...
Consider the identical balls released from rest on tracks A and B, as shown. When they reach the right ends of the tracks, which will have the greater speed? Why is this question easier to answer...
You are standing on the top of a building and throw a ball vertically upward. After 2 seconds, the ball passes you on the way down, and 2 seconds after that, it hits the ground below. a. What is the...
In Exercises 35 through 42, the slope f(x) at each point (x, y) on a curve y = f(x) is given along with a particular point (a, b) on the curve. Use this information to find f(x). 2 f(x) = x - 1/1/ +...
Rework Exercise 41 for a situation with spill thickness (T and r in feet) and radius of containment 9 feet. Data from Exercises 41 A ruptured pipe in an offshore oil rig produces a circular oil slick...
A pneumotachograph is a device used by physicians to graph the rate of air flow into and out of the lungs as a patient breathes. The graph in the accompanying figure shows the rate of inspiration...
If you purchase a $1000 par value bond for $1065 that has a 6 3/8% coupon rate and 15 years until maturity, what will be your annual return? 5.5% 5.9% 5.7% 6.1%
Famas Llamas has a weighted average cost of capital of 8.8 percent. The companys cost of equity is 12 percent, and its pretax cost of debt is 6.8 percent. The tax rate is 22 percent. What is the...
The common stock of a company paid 1.32 in dividens last year. Dividens are expected to gros at an 8 percent annual rate for an indefinite number of years. A) If the company's current market price is...

The idea of the average value of a function, discussed earlier for functions of the form y

Question:

[] f (x, y) dx dy, R A

Step by Step Answer:

x y e 2xy 1 x 2 2 y 3 The area of region R is A 2 ...View the full answer

Calculus With Applications

Students also viewed these Mathematics questions