The idea of the average value of a function, discussed earlier for functions of the form y

Question:

The idea of the average value of a function, discussed earlier for functions of the form y = f (x), can be extended to functions of more than one independent variable. For a function z = f (x, y), he average value of f over a region R is defined as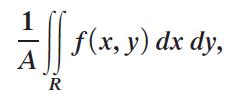

where A is the area of the region R. Find the average value for each function over the regions R having the given boundaries.

ƒ(x, y) = x² + y²; 0 ≤ x ≤ 2, 0 ≤ y ≤ 3

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Calculus With Applications

ISBN: 9780135871348

12th Edition

Authors: Margaret L. Lial

See More Books

Question Posted: Jan 19, 2023 03:13 AM

See More Questions

In which direction will each compass point when there is a large current in the direction shown? In which direction will each compass point when there is a large current in the direction shown? The...
The idea of the average value of a function, discussed earlier for functions of the form y = f (x), can be extended to functions of more than one independent variable. For a function z = f (x, y), he...
The idea of the average value of a function, discussed earlier for functions of the form y = f (x), can be extended to functions of more than one independent variable. For a function z = f (x, y), he...
Required Use the Target Corporations annual report in Appendix B to answer the following questions. a. What was Targets current ratio for its fiscal-year ended February 1, 2014 (2013) and 2012? b....
Describe the steps that might be required in writing and producing a play. Compare these steps to the three steps for new-product development described in Section 3.2. Is there a correspondence?
What similarities do you see between our discussion here of the residual income calculation and our discussion in Chapter 8 of net present value?
What are some examples of specific needs suggested by Maslows hierarchy of needs?
Columbia Paper has the following stockholders equity account. The firms common stock has a current market price of $30 per share. Preferred stock .............$100,000 Common stock (10,000 shares at...
Current Attempt in Progress Marigold Corp. uses the perpetual inventory and the gross method. On March 1 , it purchased $ 4 7 0 0 0 of inventory, terms 2 / 1 0 , n 3 0 . On March 3 , Marigold...
The surface area of a human (in square meters) has been approximated by A = 0.024265h 0.3964 m 0.5378 , where h is the height (in cm) and m is the mass (in kg). (a) Find the approximate change in...
Use the total differential to approximate each quantity. Then use a calculator to approximate the quantity, and give the absolute value of the difference in the two results to 4 decimal places. V4.06...
Write an expression for a transverse harmonic wave that has a wavelength of 2.6 m and propagates to the right with a speed of 14.3 m/s. The amplitude of the wave is 0.11 m, and its displacement at t...
Air at $1 \mathrm{~atm}$ and $25^{\circ} \mathrm{C}$ flows in a 4-cm-diameter glass pipe at a velocity of $7 \mathrm{~m} / \mathrm{s}$. The friction factor for this flow is (a) 0.0266 (b)...
Find the regime of the boundary layer at the location of $0.1 \mathrm{~m}$ from the leading edge of an aerofoil, if the airspeed is $80 \mathrm{~ms}^{-1}$, and air condition is at that of sea...
``Nuclear Deterrence,'' by Harvey A . Smith, UMAP327. The author analyzes the stability of the arms race, assuming objectives similar to those suggested by General Taylor. The module develops...
A saturated vapor feed at $1000.0 \mathrm{kmol} / \mathrm{h}$ of methanol $(5.0 \mathrm{~mol} \%)$ and water $(95.0 \mathrm{~mol} \%)$ is fed to a distillation column with 18 stages plus a...
Use the partition functions in Equations 1.98, 1.99, and 1.100 to find the translational, rotational, and vibrational contributions to the average energy of a diatomic molecule. Compare each result...
Two people of the same weight climb a flight of stairs. The first person climbs the stairs in 30 s, and the second person climbs them in 40 s. Which person does more work? Which uses more power?
Let (x) = x 2 - 9, g(x) = 2x, and h(x) = x - 3. Find each of the following. (((--) 2
After t months on the job, a postal clerk can sort Q(t) = 700 400e 0.5t letters per hour. What is the average rate at which the clerk sorts mail during the first 3 months on the job?
In Exercises 35 through 42, the slope f'(x) at each point (x, y) on a curve y = f(x) is given along with a particular point (a, b) on the curve. Use this information to find f(x). f'(x) = 4x + 1; (1,...
In Exercises 3 through 36, find the indicated integral and check your answer by differentiation. 1 x(x + 1) dx
In 2019, Sunland Company had a break-even point of $388,000 based on a selling price of $5 per unit and fixed costs of $155,200. In 2020, the selling price and the variable costs per unit did not...
11. String Conversion Given a binary string consisting of characters '0's and '1', the following operation can be performed it: Choose two adjacent characters, and replace both the characters with...
Consider the table shown below to answer the question posed in part a. Parts b and c are independent of the given table. Callaway Golf (ELY) Alaska Air Group (ALK) Yum! Brands (YUM) Caterpillar...

The idea of the average value of a function, discussed earlier for functions of the form y

Question:

[] f (x, y) dx dy, R A

Step by Step Answer:

x y x 2 y 2 0 x 2 0 y 3 The area of region R ...View the full answer

Calculus With Applications

Students also viewed these Mathematics questions