The logistic equation introduced in Section 1, can be written as where c and p are positive
Question:
The logistic equation introduced in Section 1,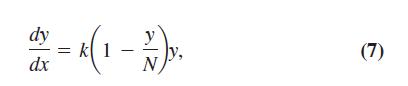
can be written as
where c and p are positive constants. Although this is a nonlinear differential equation, it can be reduced to a linear equation by a suitable substitution for the variable y.
(a) Letting y = 1/z and dy/dx = (-1/z2)dz/dx, rewrite Equation (8) in terms of z. Solve for z and then for y.
(b) Let z(0) = 1/y0 in part (a) and find a particular solution for y.
(c) Find the limit of y as x→ ∞. This is the saturation level of the population.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





