We claim that Equation (1) is a solution of the differential equation where t measures time from
Question:
We claim that Equation (1) is a solution of the differential equation
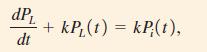
where t measures time from the present. The constant k = r/V measures how quickly the water in the lake is replaced through inflow and corresponding outflow. The constant pL(0) is the current pollution level.
a. To show that Equation (1) does define a solution of the differential equation, multiply both sides of Equation (1) by ekt and then differentiate both sides with respect to t. Remember from the section on the Fundamental Theorem of Calculus that you can differentiate an integral by using the version of the Fundamental Theorem that says
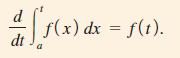
b. When you substitute t = 0 into the right-hand side of Equation (1), you should get pL(0). Do you? What happens to the integral? What happens to the factor of e–kt?
c. The map indicates a value of 30.8 for Lake Michigan. What value of k does this correspond to? What percent of the water in Lake Michigan is replaced each year by inflow? Which lake has the biggest annual water turnover?
Equation 1
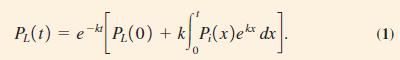
Step by Step Answer:

Calculus With Applications
ISBN: 9780321831101
10th Edition
Authors: Margaret L Lial, Raymond N Greenwell, Nathan P Ritchey





