We saw that the acceleration of gravity is a constant if air resistance is ignored. But air resistance cannot always be ignored, or parachutes would be of little use. In the presence of air resistance, the equation for acceleration also contains a term roughly proportional to the velocity squared. Since acceleration forces a falling object downward and air resistance pushes it upward, the air resistance term is opposite in sign to the acceleration of gravity. Thus,

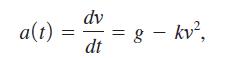
where g and k are positive constants. Future calculations will be simpler if we replace g and k by the squared constants G² and K², giving

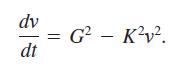
(a) Use separation of variables and the fact that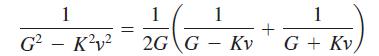

to solve the differential equation above. Assume v < G/K, which is certainly true when the object starts falling (with v = 0). Write your solution in the form of v as a function of t.

(b) Find lim_t→∞v(t), where v(t) is the solution you found in part (a). What does this tell you about a falling object in the presence of air resistance?

(c) According to Harper’s Index, the terminal velocity of a cat falling from a tall building is 60 mph. Use your answers from part (b), plus the fact that 60 mph = 88 ft per second and g, the acceleration of gravity, is 32 ft per second2, to find a formula for the velocity of a falling cat (in ft per second) as a function of time (in seconds).

Transcribed Image Text:

a(t) dv dt = 8 - kv²,