A tank containing water is in the form of a cone with vertex C. The axis is vertical and the semi-vertical angle is 60°, as shown in the diagram. At time t = 0, the tank is full and the depth of water is H. At this instant, a tap at C is opened and water begins to flow out. The volume of water in the tank decreases at a rate proportional to √h where h is the depth of water at time t. The tank becomes empty when t = 60.

i. Show that h and t satisfy a differential equation of the form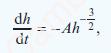where A is a positive constant.

ii. Solve the differential equation given in part i and obtain an expression for t in terms of h and H.

iii. Find the time at which the depth reaches 1/2H.

Transcribed Image Text:

dh dt 11 m/a 3 -Ah 2,