Consider the linear logit model (5.5) for an I 2 table, with y i a bin(n i , i ) variate. a. Show

Consider the linear logit model (5.5) for an I × 2 table, with y_i a bin(n_i, π_i) variate.

a. Show that the log likelihood is

b. Show that the sufficient statistic for β is ∑_iy_i x_i, and explain why this is essentially the variable utilized in the Cochran–Armitage test. (Hence that test is a score test of H₀: β = 0.)

c. Letting S = ∑_i y_i show that the likelihood equations are

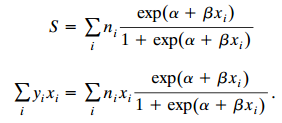
d. Let {µ̂_i = n_i π̂_i}. Explain why ∑_i µ̂_i = ∑_i y_i and

Explain why this implies that the mean score on x across the rows in the first column is the same for the model fit as for the observed data. They are also identical for the second column.